Algorithm: Efficiency and Analysis
Algorithm
Efficiency
Algorithmic efficiency
is the properties of an algorithm which relate to the amount of resources used by the algorithm.
An
algorithm must be analyzed to determine its resource usage. And so to get maximum
efficiency we need to minimize resource usage. And these resources are Time and Space.
Algorithms
is considered to be more efficient often depends on high speed, or for minimum
memory usage. An algorithm is considered efficient if its resource consumption
(or computational cost) is at or below some acceptable level. Roughly speaking,
'acceptable' means: will it run in a reasonable amount of time on an available
computer [1].
Measures
of resource usage
Ø The two
most common measures are:
Time: How long
does the algorithm take to complete.
Space: How much
working memory (typically RAM) is needed by the algorithm. This has two
aspects: the amount of memory needed by the code, and the amount of memory
needed for the data on which the code operates.
Ø For
computers whose power is supplied by a battery (e.g. laptops), or for very
long/ large calculations (e.g. supercomputers), other measures of interest are:
F Direct power consumption: Power
needed directly to operate the computer.
F Indirect power consumption: Power
needed for cooling, lighting, etc.
Ø In some
cases other less common measure may also be relevant:
F Transmission size: Bandwidth
could be a limiting factor. Data compression can be used to reduce the amount
of data to be transmitted. Displaying a picture or image (e.g. Google logo) can
result in transmitting tens of thousands of bytes (48K in this case) compared
with transmitting six bytes for the text "Google" [1].
F External space: space
needed on a disk or other external memory device; this could be for temporary
storage while the algorithm is being carried out, or it could be long-term
storage needed to be carried forward for future reference [1].
F Response time: this is
particularly relevant in a real-time application when the computer system must
respond quickly to some external event [1].
Ø Implementation
issues can also have an effect on actual efficiency, such as the choice of
programming language, or the way in which the algorithm is actually coded, or
the choice of a compiler for a particular language, or the compilation options
used, or even the operating system being used.
Algorithm
Complexity
“The complexity of an algorithm is the cost to use the algorithm to solve a
problem.”
The cost can be
measured in terms of
F Executed
Instructions (the amount of work the Algorithm does)
F Running
Time
F Memory
Consumption etc..
Thus the Algorithm complexity is a measure of the
algorithms resource demands, it’s not about how hard the algorithm is to
understand!
The most interesting resource seems a running time,
but is it the good measure?
The running time of an algorithm depends on many
things:
·
The programmer’s skill and the
programming language.
·
The computers machine language.
·
The code that the compiler generates.
·
The size of the problem (e.g. no. of
inputs).
·
The nature of input (sorted/unsorted).
·
The method chosen.
Elementary
Operations
The work algorithm
does, can be referred as the Elementary
Operations.
Elementary
operations are assumed to require one time unit e.g. it’s an operation
whose complexity can be bounded by a constant.
Complexity
is a relative concept, only interesting together with the corresponding elementary
operation.
Following are some
examples of problems, its size and Elementary operations.
Analyzing
Control Statements
Here
we start by presenting the INSERTION-S ORT procedure with the time “cost” of each statement and the number
of times each statement is executed. For each j = 2, 3, ..., n, where n = A:
length, we let tj denote
the number of times the while loop test in line 5 is executed for that value of
j. When for or while loop exits
in the usual way (i.e., due to the test in the loop header), the test is
executed one time more than the loop body. We assume that comments are not
executable statements, and so they take no time.
Here
in algorithm, cost (c1, c2, …, cn) shows the
time taken by that particular operation and time shows the number of times the statement
executes.
So
the running time T(n) of Insertion Sort
on n values, we sum the product of cost and times column.
From Series Math,
So,
Thus
we can express this worst-case running time as an2 + bn + c for constants a, b, and c that again depends
on the statement costs ci, it is thus a quadratic function of n.
Asymptotic Notation, Complexity Class Theory, Average and Worst Case Analysis and Algorithm Analysis are explained in very simple manner in PDF files provided here. Kindly download the PDF and go through it!



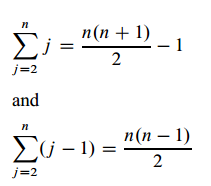

No comments:
Post a Comment