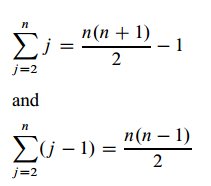Recurrences Solving
Recurrence
Relations
- A recurrence relation is an equation which is defined in terms of itself.
- Why are recurrences good things?
–
Many natural
functions are easily expressed as recurrences:
•
an = a n-1 + 1, a1 =
1--> an = n
(polynomial)
•
an = 2a n-1 ,a1 = 1--> an = 2n (exponential)
•
an = na n-1 ,a1 = 1--> an = n! (weird fun)
- It is often easy to find a recurrence as the solution of a counting problem.
- Recursion is Mathematical Induction!
- In both, we have general and boundary conditions, with the general condition breaking the problem into smaller and smaller pieces.
- The initial or boundary condition terminates the recursion.
Recurrence
Solving
There are 3 general methods for solving recurrences
Substitution: Guess & Verify:
Guess a solution
and verify: It is correct with an inductive proof.
Recurrence Tree Method: Draw a recurrence tree and calculate the
time taken by every level of tree.
Master
Theorem: If the recurrence has the form T(n) =aT
(n/b) +f(n), then there is a formula that can (often) be applied.
1) Substitution Method: We make a guess for the solution and then we use
mathematical induction to prove the the guess is correct or incorrect.
For example consider the recurrence T(n) = 2T(n/2) + n
We guess the solution as T(n) = O(nLogn). Now we use
induction
to prove our guess.
We need to prove that T(n) <= cnLogn. We can assume that
it is true
for values smaller than n.
T(n) = 2T(n/2) + n
<= cn/2Log(n/2)
+ n
= cnLogn - cnLog2 + n
= cnLogn - cn + n
<= cnLogn
2) Recurrence Tree
Method: In this method, we draw a recurrence tree and calculate the
time taken by every level of tree. Finally, we sum the work done at all levels.
To draw the recurrence tree, we start from the given recurrence and keep
drawing till we find a pattern among levels. The pattern is typically a
arithmetic or geometric series.
For example consider the recurrence relation
T(n) = T(n/4) + T(n/2) + cn2
cn2
/ \
T(n/4) T(n/2)
If we further break down the expression T(n/4) and T(n/2), we get following recursion tree.
cn2
/ \
c(n2)/16 c(n2)/4
/ \ / \
T(n/16) T(n/8) T(n/8) T(n/4)
Breaking down further gives us following
cn2
/ \
c(n2)/16 c(n2)/4
/ \ / \
c(n2)/256 c(n2)/64 c(n2)/64 c(n2)/16
/ \ / \ / \ / \
To know the value of T(n), we need to calculate sum of tree nodes level by level. If we sum the above tree level by level, we get the following series T(n) = c(n^2 + 5(n^2)/16 + 25(n^2)/256) + ....
The above series is geometrical progression with ratio 5/16.
To get an upper bound, we can sum the infinite series.
We get the sum as (n2)/(1 - 5/16) which is O(n2).
3)
Master Method:
Master
Method is a direct way to get the solution. The master method works only for
following type of recurrences or for recurrences that can be transformed to
following type.